BLOG ARTICLE prime number | 2 ARTICLE FOUND

  1. 2009.01.28 [Python example] 소수 구하기 #2 (에라토스테네스의 체)
  2. 2009.01.11 [Python example] 소수 구하기

[Python example] 소수 구하기 #2 (에라토스테네스의 체)

개발/python 2009. 1. 28. 00:15
이번에는 소수를 구하는 또다른 방법을 구현해 보겠습니다.

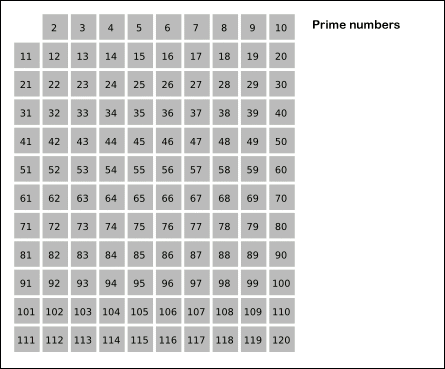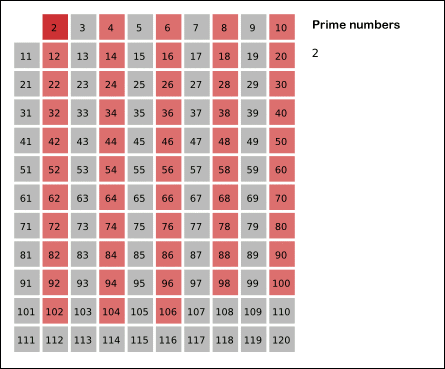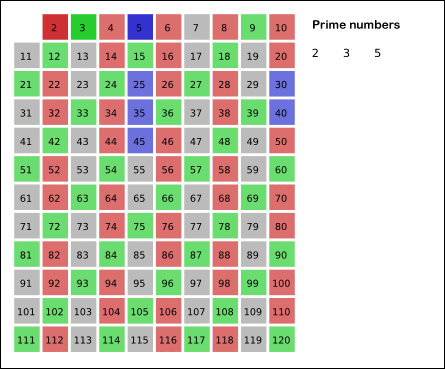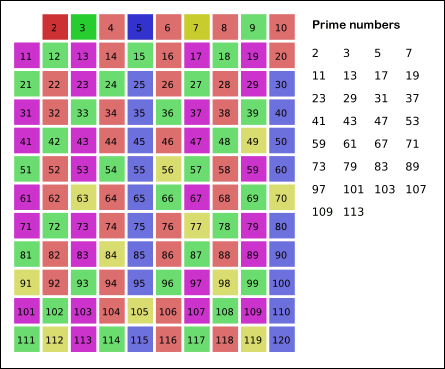
소수는 예전에 구한 방법 이외에도, '에라토스테네스의 체'라는 방법을 이용해서 구할 수도 있습니다.


그림출처: http://en.wikipedia.org/wiki/Sieve_of_Eratosthenes

이 알고리즘을 설명하자면,
  1. 2에서부터 n까지의 수를 체에 넣고,
  2. 체에서 가장 작은 값을 소수로 체크하고, 그 수의 배수들을 모두 제외시킵니다.
  3. 위 2번 과정을 반복합니다.

여러가지 방법을 사용할 수 있겠지만, 딕셔너리를 이용해서 구현하면 다음과 같습니다.

# -*- coding: utf-8 -*-
import sys

if __name__=="__main__":
    print( sys.version )
    N = int( input("input a number : ") )
    #init
    sieve = {}
    for i in range(2, N+1):
        sieve[i] = 0
       
    # Sieve of Eratosthenes
    for i in range(2, N+1):
        if sieve[i]==0:
            n=2
            while i*n <= N:
                sieve[i*n]=1
                n+=1

    #print results
    for i in range(2, N+1):
        if sieve[i]==0:
            print( i, end="," )
    print()       
    input("press any key")

100을 넣고 실행해 보면 결과는 다음과 같습니다.

3.0 (r30:67507, Dec  3 2008, 20:14:27) [MSC v.1500 32 bit (Intel)]
input a number : 100
2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59,61,67,71,73,79,83,89,97,
press any key


AND

[Python example] 소수 구하기

개발/python 2009. 1. 11. 11:50
소수는 1과 자신 이외의 약수를 갖지 않는 정수를 이야기 합니다.
정수를 입력 받아 그 수가 소수인지 아닌지 검사하는 프로그램을 짜 봅시다.

다음과 같이 소수의 정의대로 2에서부터 입력받은 n-1까지 순회하며 나누어 떨어지는지 아닌지 검사하면 간단히 해결됩니다.

import sys
import math

def isPrime(n):
    bPrime = True
    for i in range(2,int(math.sqrt(n))+1):
        if n%i==0:
            bPrime = False
            break
    return bPrime

if __name__=="__main__":
    print( sys.version )
    N = input("input a number : ")
    if isPrime(int(N)):
        print("prime number")
    else:
        print("not prime number")
    input("press any key")

실행해 보면 다음과 같이 동작하는 것을 알 수 있습니다.

3.0 (r30:67507, Dec  3 2008, 20:14:27) [MSC v.1500 32 bit (Intel)]
input a number : 30
not prime number
press any key

3.0 (r30:67507, Dec  3 2008, 20:14:27) [MSC v.1500 32 bit (Intel)]
input a number : 13
prime number
press any key

그러나 이 예제에는 약간 비효율적인 면이 있는데요.
소수검사는 2에서부터 n-1까지 할 필요가 없습니다. 2에서부터 sqrt(n)까지만 하면 충분하죠.
즉 아래와 같이 isPrime 함수를 변경하면 속도가 약간 더 빠르게 됩니다.

import math

def isPrime(n):
    bPrime = True
    for i in range(2,int(math.sqrt(n))+1):
        if n%i==0:
            bPrime = False
            break
    return bPrime

AND

티스토리툴바